False success

Teachers make naive assumptions all the time. They believe that students are interested, while they are merely polite. It’s even worse for teachers’ trainers, because the salaries and careers of the future teachers are at stake.

There are very self-suficient trainers (in France) who are despised by the majority of their trainees, because the organization of the formation itself is an incentive to hypocrisis. On forums, the youngsters are masssively advised to lie during their training, to do whatever is required from them during their first year, and after graduating to act according to their conscience. As a monitor myself, I’m not fully confident in that regard. Are you merely polite, when you agree with me?

Figure out carrefuly what you’re actually measuring when you evaluate your own students.

Repetiton

They don’t read, they repeat. It’s a major issue at grade 1 (and for some students much later than grade 1). The teacher makes them “read” words or sentences on the board. Except for the very first student, it’s possible to do the exercise merely by repeating what the others have said, without paying attention to the letters that constitute the words. That bias exists with any method, but is much more likely with a whole language approach. We see pupils who can recite by heart whole pages of their textbook, but are stuck before the most simple sentence in the street. Many of them only recognize parts of words and fill the gaps by guessing. I remember a class at sixième (grade 7 or so). I asked them to read aloud a page of Pinocchio. The first one replaced 10 words in a single paragraph. He didn’t read what was written, but invented those words. Sometimes, it was a word of similar form, (usually the same beginning), sometimes it was a synonym. Instead of reading carefully, he used the context to guess. What frightened me was that the second pupil had the same problem, and the third and so on. It was not some kind of disability, but clearly the result of a bad teaching. You don’t see an epidemy like that without a common cause. I’m pretty sure that their teacher in the primary school was confident on their abilities. But I used a slightly different way to evaluate them, by presenting them with a brand new text adapted for children, and the results were dramatically different.

At the baccalauréat, in Latin, most of the applicants merely memorize the traduction of the text they are supposed to translate again. From time to time, one of them recites the wrong text. It’s logical. As we have dismissed the systematic teaching of grammar and vocabulary, they have to relie on something else.

Repeating doesn’t mean understanding, of course. At least, make the students rephrase the lesson or define words or give several examples. Beware that the student you question doesn’t repeat your own example and that rephrasing could lead to losses in accuracy. It is often necessary to learn a definition or a theorem by heart. But it is also necessary to make the students apply the theorem to various situations, in order to be sure that they understand it.

We would agree on the fact that it is unfair to evaluate a student on something that has not been taught to him previously. But you can’t test their understanding just by making them repeat the very same exercise. You have to alter the context to force them to think a little bit.

Context

Young children are very good at memorizing series: alphabet, mutiplication tables and so on. Even if memorization of series is actually useful (for instance alphabetic order to search in a dictionary), it isn’t the main objective. One have to recognize a letter in any context, all the time, not only in series. And you need to recognize it perfectly without hesitation. You can’t recite the entire table of 2 each time you need a partial answer, if you are to calculate 2682 × 322.

Teachers should always alternate the memorization of series with random recognition of the elements of the series and use them in context.

It’s generally recommended to make a lesson in three parts: contextualisation, decontextualisation, recontextualisation. Those words are impressive, but it’s quite simple in fact. Always begin with a concrete and meaningful example. Before you explain the theorem of Thales, expose a problem. You want to know the height of a tree without climbing on it, in order to know if it’s interesting to chop it down. And you show how to calculate it using geometry. That contextualisation. Then you explain the theorem in its general and abstract formulation. That’s decontextualisation. It means that you have a rule you can use in many different situations, it doesn’t have to be a tree. It doesn’t have to be vertical etc. Finally, you make exercises to apply the rule to other situations, for instance, calculate the width of the river you want to cross with the lumber you’ve cut (although it would be more logical to begin the lesson with the last example). That’s recontextualisation.

Notice that some students are very bad at understanding examples (that they are only examples) or at changing the context. When you do your lesson, it’s good to give several simple examples, in order to show what’s different in them and what is the pattern you want the students to understand.

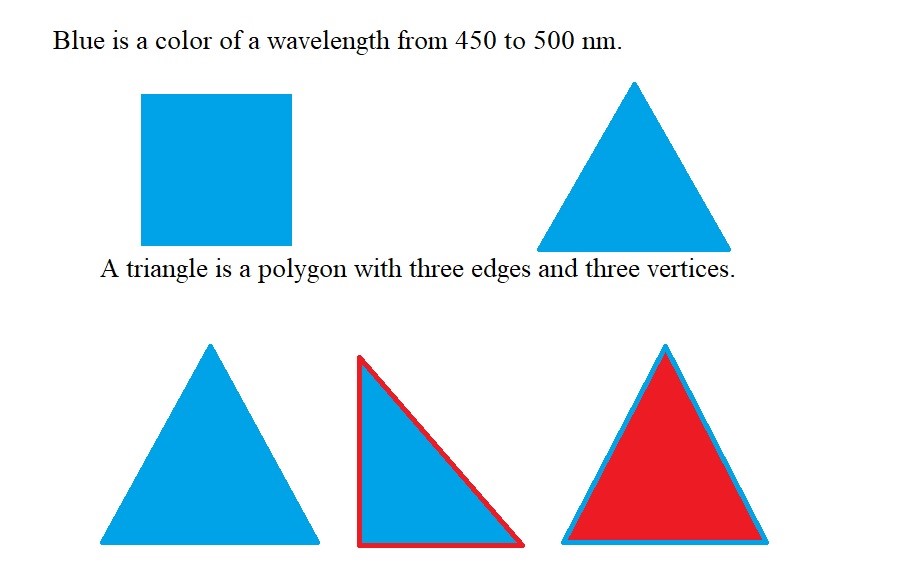
You need a blue triangle and a blue square to explain that blue is a color and you’re not interested in the shape.

You need a blue triangle and a red triangle, to explain the concept of triangle, with young children. In fact, the definition, as a polygon with three edges and three vertices is not very useful at first, because you need triangles or other simple shapes to explain what edges and vertices are. And polygon is so weird a word!

 

Implied answers

The mistake is frequently made orally, less so in written.

“Do you think that big army has won the battle?” Well, if you ask the question, probably not.

Implied answers are also a technic to influence people and force them to say things they don’t actually believe.

Sometimes, the answer is implied by the structure of the question.

For instance:

Complete with enough, too, not… enough

We did … have … money to go to the castle.

We expect a solution in two parts. The solution is obvious, even if you don’t understand the sentence.

Sometimes answers are given in a series of questions

It frequently happens, when we try to organize tests around complex and meaningful tasks, but we can’t just let the students do all the process by themselves. In a step by step test, it difficult to formulate a question without using the result of the previous one.

Compensation strategies

Sometimes, students who don’t know the academic method to solve a problem are able to figure out another solution. It’s interesting because they are thinking. It’s often seen with very smart students who are poorly educated.

The problem is that home-made solutions often require a huge cognitive load. For instance, a pupil in primary school doesn’t know the algorithm to solve a division, but manages to find the answer by making a series of substractions. “If you have 25 marbles. You give packs of 5 marbles to your classmates. How many of them receive a pack?”

25÷5 = 5

5=5

Or

25-5=20

20-5=15

15-5=10

10-5=5

5-5=0

He’s made 5 operations, so the answer is 5.

The answer is accurate. The reasoning is good. But it’s time-consuming. Imagine what would happen to the same student, if he has to calculate

1, 200, 000÷10

Always make the students write down their reasoning or explain it oraly, even if the answer is good!

If the reasoning is not the one you expected, but is logically valid, first praise the kid. He’s been clever. Then, if his reasoning is better than yours, admit it, applaud. He deserves it. If it is not (because it’s time consuming for instance), or if he just has to learn your technic in order to be prepared for other problems, propose the more efficient method as an intersting alternative, without despising his own.

If the reasoning is not accurate and the answer was found by chanc, it’s essential to demonstrate why it isn’t accurate. For instance, find another example for which his method doesn’t work. I know it’s difficult to improvise such demonstration, but it’s important. The student who has found the same result as you tends to believe that his “solution” his also valid. He consider it as a “proof” and disbelieves the teacher who only disagrees.

Pure force

I remember a game on computer that was supposed to help pupils learn reading. It was part of a whole language method but it isn’t the point. The game was a quizz with 4 possible answers to each question. The problem was that the question was reset whenever the answer was wrong. Only the last question. Therefore, it was possible to score and beat the machine by pure force, without reading at all, just by trying successively all the possibilities. A little flaw in the game concept made it absolutely useless. It took me only a minute or so to spot the flaw, but the trainer didn’t see it. It requires some habit of critical thinking to figure out such an issue.

Quotations

In Language tests, they often use quotations as answers. The students are required to find, in a text, the sentence that answers the question. The idea behind this exercise is to test the reading skill alone, and avoid penalizing the one who is bad at writting. It’s a major flaw. It’s generally possible to find out the sentence where the solution must be, just by comparing words, without understanding anything. Many students compensate for their lack of knowledge with some cunning. I even managed to do it with languages I had never studied at all (like Spanish). That flaw is obvious to experienced teachers, but not to bureaucrats. By the way, we are talking about the baccalauréat in France (professional series).

Even though it’s recommended by many expert to not translate (because word by word thinking lead to mistakes and because no word has an accurate translation in a foreign language), it’s safer to make the student translate into his native tongue in order to check whether he has understood the text. It’s especially useful when he lacks the vocabulary to rephrase in the foreign language.

Collective success, individual failure

“Do you remember the previous lesson?”

If asked to the entire class, that question has no value to assess the work of the students. In fact, it’s very likely that over 30 students at least one will be able to answer. It doesn’t mean that the other 29 have understood anything. Question several students randomely. They don’t have to be volunteers. It’s a lesson! They know what they had to do. Of course, make sure that the notebooks are closed.

When the students repeat a foreign sentence in chorus, it’s impossible to be sure of the accuracy. Besides the chant isn’t natural. It has no structure and breaks the normal rhythm of the sentences.

I dont mean you must despise it, because it’s a good drill, and it’s very useful to recall the attention of the students. At least, everybody works.

But you must alternate with individual questioning.

For instance, an exercise of pronunciation.

“Please repeat: fox!”
“Altogether!” 3 times
“Dara” 2 times
“Vannyda” 3 times
“Panha” 1 time
“Altogether!” 2 times.

Expected success rates

It’s important to understand the meaning of the scores obtained by the students. When they pass a MCQ test, the most probable success rate if they answer randomely is not 0. If there are 4 choices, it’s 25%. Don’t be fooled by a 50% success rate. It isn’t good. It’s very bad. There are solutions to mark those tests properly. It would be too technical to explain it here, but you can check this page.

The figure is even worse with true or false questions.

With MCQs, it’s generally possible to make a decent score just by eliminating improbable or illogical choices. A clever and lazy student can make illusion in most cases.

By the way, it’s interesting to use that method at your advantage and do a good lesson on critical thinking. Train the students to spot false information, to calculate orders of magnitude and so on. It’s very useful in daily life. It helps to get rid of liars and crooks.